Brilliant Strategies Of Info About How To Tell If Planes Are Parallel Or Orthogonal

Parallel Planes
Unraveling the Mystery
1. Understanding Plane Relationships
Ever stared up at a perfectly aligned set of shelves or noticed how a building's walls meet and wondered about the geometry at play? Turns out, understanding whether planes are parallel or orthogonal isn't just for architects and mathematicians! It's a fundamental concept in geometry, and trust me, it's not as intimidating as it sounds. We're going to break it down in a way that's easy to grasp, even if your last brush with geometry was trying to remember the Pythagorean theorem (a + b = c, remember that?).
Think of planes as infinitely large, flat surfaces, like an endless piece of paper extending in all directions. The key to figuring out their relationship lies in understanding their normal vectors. A normal vector is simply a vector that is perpendicular (at a 90-degree angle) to the plane. Imagine sticking a straight pin perfectly upright into that piece of paper — that's essentially what a normal vector does.
Now, the real magic happens when we compare the normal vectors of two different planes. If those normal vectors are pointing in the exact same (or opposite) direction, then the planes are parallel. Think of two slices of bread perfectly aligned in a loaf. If the normal vectors are perpendicular to each other, the planes are orthogonal, meaning they intersect at a right angle. Picture the walls and floor of a typical room.
But how do we actually determine if these normal vectors are pointing in the right directions? Thats where a little vector algebra comes in, but dont worry, we'll make it painless and (dare I say) even a little bit fun! We'll skip the super complicated stuff and focus on the practical methods you can use.

Solved Determine If The Following Planes Are Parallel,
Decoding Normal Vectors
2. Finding and Using Normal Vectors
Okay, so we know normal vectors are important, but how do we actually find them? This depends on how the equation of the plane is presented to you. The most common way is in the form Ax + By + Cz = D, where A, B, and C are constants. In this case, the normal vector is simply (A, B, C). Yep, that's it! The coefficients of x, y, and z directly give you the components of the normal vector. For example, if a plane is described by 2x + 3y - z = 5, its normal vector is (2, 3, -1).
If you're given three points on a plane, things get a little trickier, but not impossible! You need to create two vectors that lie within the plane. You can do this by subtracting the coordinates of one point from the coordinates of the other two. For instance, if you have points P, Q, and R, you can create vectors PQ and PR. Once you have these vectors, you can find the normal vector by taking their cross product. The cross product is a vector that is perpendicular to both PQ and PR, and thus, perpendicular to the plane itself.
Remember that the normal vector is not unique. Any scalar multiple of a normal vector is also a normal vector. This just means you can multiply the components of the normal vector by any number (except zero), and it will still be perpendicular to the plane. This is important when comparing normal vectors, as they might look different but still represent the same direction. For example, (2, 4, 6) and (1, 2, 3) both represent the same direction.
Once you've extracted (or calculated) the normal vectors for the two planes, you're ready to put them to the test! This is where we determine if they're parallel or orthogonal.
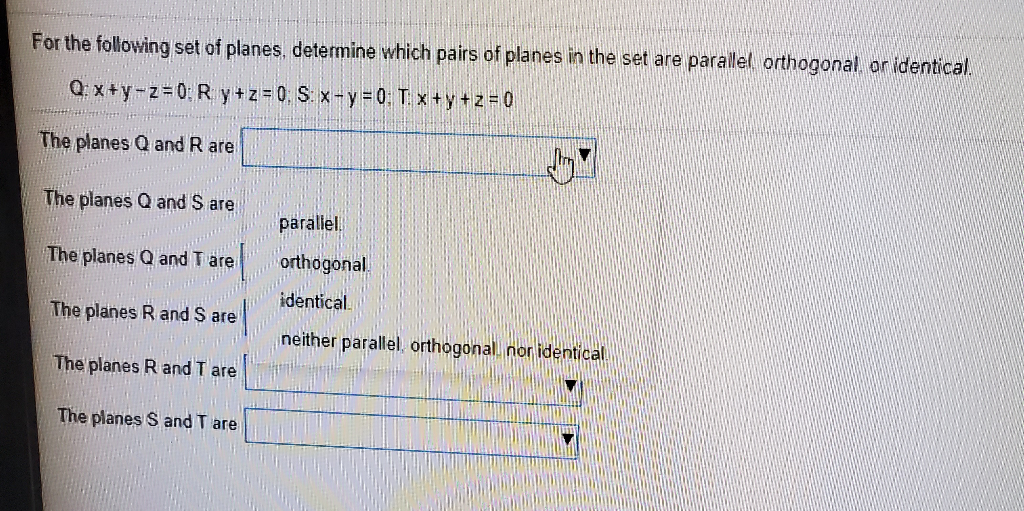
Solved For The Following Set Of Planes, Determine Which
The Dot Product Test
3. Using the Dot Product to Check for Parallel Planes
So, how do we figure out if two vectors are parallel? The key is the dot product. The dot product of two vectors (let's call them u and v) is a scalar value calculated as: u v = |u| |v| cos(), where |u| and |v| are the magnitudes (lengths) of the vectors, and is the angle between them. Now, here's the cool part: if the vectors are parallel (or anti-parallel, meaning they point in opposite directions), the angle is either 0 or 180. The cosine of 0 is 1, and the cosine of 180 is -1.
In practice, instead of calculating the angle directly, we check if one vector is a scalar multiple of the other. This means you can multiply one vector by a constant to get the other vector. For example, if vector u is (1, 2, 3) and vector v is (2, 4, 6), then v = 2u. Therefore, u and v are parallel.
Another way to check for parallelism using the dot product is as follows: If the two vectors are parallel, the dot product will be equal to the product of their magnitudes. So, calculate the dot product of the two normal vectors. Then, calculate the magnitude of each vector. If the dot product is equal to plus or minus the product of the magnitudes, the planes are parallel (or anti-parallel, which we still consider parallel in this context).
Lets say our two planes have normal vectors n1 = (1, 0, 0) and n2 = (2, 0, 0). You can clearly see that n2 = 2 n1, so they are parallel. Alternatively, calculating the dot product: n1 n2 = (1 2) + (0 0) + (0 0) = 2. The magnitudes are |n1| = 1 and |n2| = 2. The product of the magnitudes is 1 2 = 2, which is equal to the dot product. Thus, the vectors are parallel and so are the planes.
The Orthogonality Test: Spotting Right Angles
4. Using the Dot Product to Check for Orthogonal Planes
Now, let's talk about orthogonality. Two planes are orthogonal if their normal vectors are perpendicular, meaning they intersect at a 90-degree angle. Remember the dot product formula? If the angle is 90, then cos() = 0. Therefore, the dot product of two perpendicular vectors is zero!
This gives us a simple and elegant test for orthogonality: calculate the dot product of the normal vectors. If the result is zero, the planes are orthogonal. That's it! No need to worry about magnitudes or angles. Just calculate the dot product and check if it equals zero. This makes spotting right angles between planes a breeze.
For example, if plane A has a normal vector (1, 0, 0) and plane B has a normal vector (0, 1, 0), then their dot product is (1 0) + (0 1) + (0 0) = 0. Since the dot product is zero, the planes are orthogonal. You can visualize this as one plane being the xz-plane and the other being the yz-plane. They clearly intersect at a right angle.
If the dot product is not zero, the planes are neither parallel nor orthogonal. They intersect at some angle other than 90 degrees. It's important to remember this "neither" option, as not all planes fall neatly into the parallel or orthogonal categories.

Putting It All Together
5. Combining the Tests
Let's run through a quick example to solidify everything. Suppose we have two planes: Plane 1: 3x + 2y - z = 4, and Plane 2: 6x + 4y - 2z = 8. The normal vector for Plane 1 is (3, 2, -1) and the normal vector for Plane 2 is (6, 4, -2).
First, let's check for parallelism. We can see that (6, 4, -2) = 2 (3, 2, -1). So, the normal vectors are scalar multiples of each other, and the planes are parallel. Alternatively, we could calculate the dot product: (3 6) + (2 4) + (-1 -2) = 18 + 8 + 2 = 28. The magnitudes are |(3, 2, -1)| = 14 and |(6, 4, -2)| = 56 = 214. The product of the magnitudes is 14 214 = 2 14 = 28, which is equal to the dot product. Thus, the planes are parallel.
Now, let's say we have a different Plane 3: x - y + z = 2. Its normal vector is (1, -1, 1). Let's check if Plane 1 and Plane 3 are orthogonal. The dot product of their normal vectors is (3 1) + (2 -1) + (-1 * 1) = 3 - 2 - 1 = 0. Since the dot product is zero, Plane 1 and Plane 3 are orthogonal.
See? Its not as daunting as it first appears. With a little understanding of normal vectors and the dot product, you can easily determine whether planes are parallel or orthogonal. Now go forth and analyze all the planes you encounter! (Just kidding... unless?)
FAQ
6. Answering Your Burning Questions About Plane Relationships
Still have questions? You're not alone! Here are some frequently asked questions to further clarify the concepts we've covered.
Q: What if the dot product is neither zero nor equal to the product of the magnitudes?
A: If the dot product is neither zero nor equal to the product of the magnitudes (plus or minus), the planes are neither parallel nor orthogonal. They intersect at an angle other than 90 degrees.
Q: Does the order of vectors matter when calculating the dot product?
A: No, the dot product is commutative, meaning u v = v u. The order of the vectors does not affect the result.
Q: Are coincident planes considered parallel?
A: Yes, coincident planes (planes that lie on top of each other) are considered parallel. Their normal vectors will be scalar multiples of each other.
Q: Can these concepts be applied to higher dimensions?
A: Absolutely! While visualizing it gets trickier, the fundamental principles of normal vectors and the dot product extend to higher dimensions. You can still use these tools to determine relationships between hyperplanes in n-dimensional space.
